 El diario ABC publicaba el pasado día 6 de febrero una noticia con el siguiente titular: «Los papeles de Bárcenas son falsos, según la Ley de Benford«. El artículo, que hace referencia a los cálculos realizados por Miguel Lacruz Martin, profesor de la Universidad de Sevilla, argumenta que la supuesta contabilidad B del Partido Popular habría sido falseada por su autor. El motivo es que la distribución de su primer dígito no se ajustaría a las frecuencias que suelen observarse en diversos fenómenos socioeconómicos. En este breve post reproducimos los resultados y hacemos una interpretación cautelosa de los mismos.
El diario ABC publicaba el pasado día 6 de febrero una noticia con el siguiente titular: «Los papeles de Bárcenas son falsos, según la Ley de Benford«. El artículo, que hace referencia a los cálculos realizados por Miguel Lacruz Martin, profesor de la Universidad de Sevilla, argumenta que la supuesta contabilidad B del Partido Popular habría sido falseada por su autor. El motivo es que la distribución de su primer dígito no se ajustaría a las frecuencias que suelen observarse en diversos fenómenos socioeconómicos. En este breve post reproducimos los resultados y hacemos una interpretación cautelosa de los mismos.
¿En qué consiste la Ley de Benford (o ley del primer dígito)? La mayoría de fenómenos socioeconómicos (precios, exportaciones, cifras de población, balances de capital) que crecen continuamente en el tiempo presentan una curiosa regularidad empírica: la distribución de su primer dígito no es uniforme.
¿Qué quiere decir exactamente esto? Imagina que te pones frente a un atlas mundial y empiezas a recopilar datos de población, PIB o deuda total de los países, pero anotando solo el primer dígito de cada magnitud. Aunque en primera instancia uno creería que debería haber el mismo número de unos, doses o treses (y así hasta nueve), la realidad es que no. La cantidad de unos será mucho mayor que la de doses, y a su vez esta será mayor que la de treses. Si quiere observar esta curiosidad numérica solo tiene que hacer lo siguiente:
:: Abra una hoja de cálculo (Excel, Google Spreadsheet, OpenOffice Calc…)
:: En la casilla A1, escriba la cifra 3245 (en realidad puede ser la cifra que quiera)
:: En la casilla A2, escriba: = A1*1,05
:: A continuación, copie la casilla A2 hacia abajo tantas veces como quiera, preferiblemente más de 500
:: En la casilla B2, escriba = izquierda(A1;1)
:: Al hacer esto, extraerá el primer dígito de cada cifra
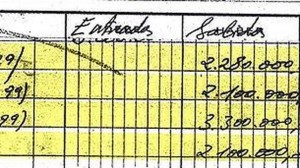
Lo que hemos hecho es crear una serie que crece a una tasa fija, en este caso al 5%. Fíjese detenidamente en lo que sucede con su serie. Cada vez que gana un dígito (por ejemplo, al pasar de 9.967 al 10.465, observará que la serie “se ralentiza” y, durante unos cuantos números (14 casos en nuestro ejemplo), el primer dígito de cada valor es el 1. Luego, la serie abandona el 1 y entra en el 2, en el que ya solo “está” en 8 casos. A continuación, sigue “acelerándose” hasta solo pasar por tres “ochos” y dos “nueves”. En cambio, al saltar otra vez a las centenas de miles vuelve a tardar 14 casos en abandonar el dígito 1. El recuento de frecuencias (que se puede obtener con la función CONTAR.SI) tiene este aspecto:
Para el que busque una explicación técnica, el fenómeno se da en procesos que llevan implícitos crecimientos de tipo exponencial, como la mayoría de fenómenos económicos. Cuando dichos fenómenos se representan en una escala logarítmica –que es la apropiada para dicho tipo de procesos-, la curiosidad numérica desaparece. Esta Ley suele usarse para saber si alguna distribución numérica que debería seguir dicha distribución no lo hace por algún error de medición o de “reporting”. Así, el fisco Estadounidense lo ha utilizado para intentar detectar casos de fraude fiscal en empresas: cuando unas cuentas se alejan sistemáticamente de dicha distribución, ello puede indicar que los números están siendo inventados.
La Ley de Benford y la presunta contabilidad B del PP
¿Qué sucede si testeamos la distribución de los papeles de Bárcenas frente a la distribución de Benford? En primer lugar, nos gustaría aclarar que replicamos el ejercicio del profesor Lacruz Martín más como un divertimento estadístico/matemático que como un intento de probar o refutar nada. El caso está siguiendo los procedimientos legales y las consecuencias se dirimirán en los tribunales.
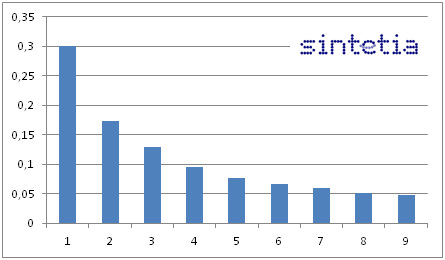
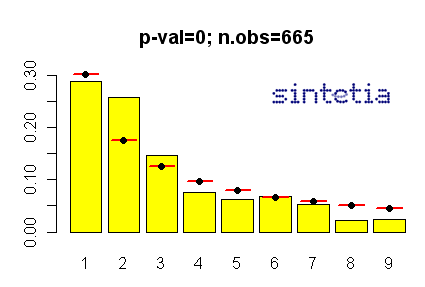
Centrémonos ahora en el ejercicio. Para empezar, acudimos a la página web de El País en la que se encuentran los datos y los copiamos en una tabla. Los hacemos legibles quitando símbolos extraños y calculamos las frecuencias relativas de los primeros dígitos. El siguiente gráfico muestra dicho cálculo. Las barras amarillas reflejan la distribución de resultados, mientras las líneas rojas horizontales reflejan la distribución teórica de Benford.
He de reconocer que los resultados sorprenden por su parecido a la distribución de Benford. No obstante, existe una anomalía en el dígito 6 que hace que la distribución no pase el test de similitud con Benford. Es decir, el test estadístico (chi-cuadrado) dice que los datos no corresponden con los de un proceso económico normal.
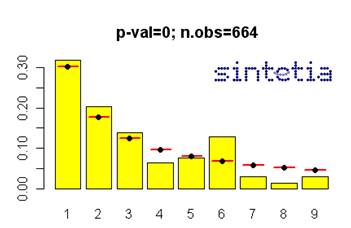
No obstante, los datos presentan una peculiaridad que merece la pena explorar. Debido al paso de la peseta al euro, muchas de las cantidades antes cercanas al millón de pesetas pasaron a expresarse en euros a partir de 2002, lo cual supuso convertir “unos” (por 1.000.000 pesetas) en “seises” (por 6.000 euros). ¿Cual sería entonces el resultado si convertimos todas las cantidades a pesetas para así no comparar distintas escalas? El resultado es el siguiente:
Al convertir todos los pagos a la misma escala, el exceso de “seises” desaparece… pero ahora tenemos un “exceso de doses”, es decir, una cantidad de pagos que empiezan en dos por encima de lo que sería normal. Ello nos lleva a una curiosidad adicional: si no hubiese tantos “doses”, la supuesta contabilidad sería, según la Ley de Benford, verídica –en el sentido de que ha tenido lugar, no en el sentido de que sea o no legal; la “Ley” de Benford entiende bien poco de temas legales-. Y, curiosamente, los supuestos pagos más comprometidos y los que más han sorprendido a la opinión pública (Rajoy, Cospedal, Oreja, etc)… ¡empiezan mayoritariamente por la cifra “dos” al expresase en pesetas!
Conclusiones
La estadística es una ciencia que rara vez nos puede aportar certezas absolutas. A menudo sirve, más bien, para descartar hipótesis descabelladas, pero la verificación de una teoría suele requerir una replicación experimental sistemática. Es por ello que, a pesar de lo que este sencillo ejercicio pueda sugerir, la Ley de Benford solo suele ser utilizada para encontrar posibles regularidades que investigar. En la medida en que el caso ya está siendo investigado por la fiscalía, poco más podemos decir. Quien quiera ver alguna certeza en dicho “exceso de doses” debe recordar que todo fenómeno real está sujeto a aleatoriedad y que ningún test estadístico es prueba irrefutable de nada.
Por lo demás, esperamos que este post pueda servir para despertar curiosidad sobre la Ley de Benford y sobre la estadística y las matemáticas en general (nota: los tests estadísticos han sido realizados con el siguiente paquete de R).
[Actualización: Puedes leer la entrada de Miguel Lacruz a la que hace referencia el ABC directamente en su blog.]
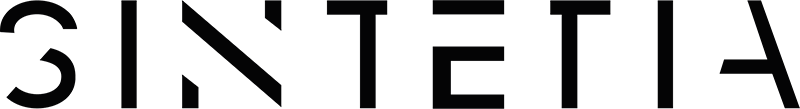

27 Comentarios
He leído el artículo con la misma cara que pone Iker Jiménez a Carmen Porter pero aún así me ha parecido muy interesante haber descubierto esta página.
Bienvenido, espero que poco a poco la cara se vuelva a su sitio, jejeje un saludo desde el equipo Sintetia
Independientemente de la aplicación que puede tener el artículo para desmontar la noticia de ABC, me parece un tema interesante que explica datos generales (económicos,demográficos…) como bien anota el autor.
Muy interesante, pero puede ser que esta distribución esté contaminada porque solo se han publicado los datos de 11 páginas. No creo que sea una muestra lo suficientemente grande para extraes estas conclusiones.
¡Me cambio de cerebro y vuelvo a leerlo!
Abel,
Me ha gustado mucho tu artículo. Ha sido buena idea cambiar a pesetas porque la ley de Benford es invariante frente a cambios de escala.
Algún lector de mi blog ha hecho el test chi cuadrado para medir la desviación de la contabilidad de Bárcenas con respecto a la ley de Benford.
Saludos,
Miguel
1º El ejercicio con la hoja de cálculo muestra que el primer dígito de un número seudoaleatorio obedece una ley de Benford.
2º Tamborete dice que tu análisis desmonta la noticia de ABC. Yo pienso al contrario, que la refuerza.
3º ¡Qué casualidad que la anomalía se produzca con los pagos más comprometedores! Razón de más para pensar que los datos han sido maquillados.
La realidades en la vida no se miden por los sucesos extraños, sino por los corrientes, y estos coinciden con la Ley de Benford
Hay que tener en cuenta que la ley de Bendford solo es aplicable si las cifras cubren varios ordenes de magnitud, es decir, si las cifras van entre 0 y 1000 – 3 ordenes de magnitud – si vale, pero si las cifras van entre 1.000.000 y 10.000.000 no vale ya que solo se cubre una orden de magnitud.
En este caso, siendo como parece sobresueldos a personas destacadas es muy posible que no cumplan ese requisito y que todas estén sobre el mismo orden de magnitud.
Por otro lado, como bien dices, es solo un indicio y lo que vale es lo que digan los tribunales.
La ley de Benford solo se cumple en digitos de crecimiento constante y acumulado, los pagos en A suelen seguir esas distribuciones (se adaptan según la inflación) los pagos en B no necesariamente.
Muy interesante todo en cualquier caso
El test no indica, ni tan siquiera sugiere vagamente, que los datos sean falsos. Indica que no siguen la distribución de Bedford. Pero esto, en una muestra tan pequeña y sobre todo tan concreta (de la actividad económica interna de unas personas determinadas, y no de todo un país y una gran empresa), no quiere decir nada. Y me explico.
Imaginad, por ejemplo, que los secretarios generales tuviesen un pacto con Bárcenas por el cual cada mes cobraran un sobresueldo de 7000 euros. Saldría, por lo tanto, un pico muy grande en el 7. ¿Eso querría decir que alguien falsificó los datos? No, querría decir simplemente que los datos no siguen la distribución porque ese pacto los está condicionando.
Igual que si sacáis la distribución de lo que cobra la gente de paro en España, supongo que saldrá un pico en el 4 porque hay cerca de un millón de personas cobrando la ayuda de 400 euros.
Para que tenga sentido aplicar un test de significatividad como éste, tiene que tratarse de datos independientes. Si agregas grandes cantidades de datos de fuentes suficientemente diversas, puedes suponer que son independientes, porque los factores distorsionadores que puede haber (como los de los ejemplos anteriores) se verán diluidos entre tanto dato. Pero si estamos hablando de una contabilidad a tan pequeña escala, ni de broma se dan las hipótesis de partida del test.
El exceso de 6 ha provocado que al convertirlos en euros haya un exceso de 2, sin embargo en la captura de la nota se ve que algunos pagos de los más comprometidos están expresados en pesetas y al convertirlos a euros pasarían a 1 (entre 12.000€ y 18.000€) y no a 2 y por tanto entrarían dentro de la distribución teórica para este dígito.
Por tanto creo que no es de recibo sugerir que los pagos más comprometedores presentan una anomalía estadística.
A mí me ha encantado, no había oído hablar de esta ley y me parece muy curiosa. Sonbretodo me ha parecido curiosa la explicación del caso de los 6, que requiere un poco de «creatividad matemática»
Está claro que deberías haber separado ambas series, precisamente por lo que muy bien has apuntado del cambio de moneda de peseta a euro.
Al dividir ambas series (una en pesetas y otra en euros) y obtener sus correspondientes dos gráficas, observarás que ahora, ni el dos, ni el seis tienen una desviación estadística significativa…
Si a esto le sumas que la Ley de Benford es una aproximación estadística que presenta en la realidad desviaciones «precisamente» en los números 2 y 6, http://upload.wikimedia.org/wikipedia/commons/thumb/8/82/Benford-physical.svg/600px-Benford-physical.svg.png lo que acabas de hacer es refutar que las seríes numéricas (aka) las cuentas de Bárcenas, son reales…
Los sobre sueldos mínimos eran de 2500 euros mensuales y muchas, muchas cantidades son de dos millones y pico de pesetas ¿¿cómo no va a predominar el 2??
Miguel,
Gracias por tus comentarios. Siento no haber citado antes tu blog (ahora ya está citado), pero no lo había encontrado en su momento; de hecho, por eso me animé a replicar el análisis.
PD: P != NP
En la web de cafematematico hay una laaarga discusión sobre este tema. Por ejemplo, acerca de realizar un Chi Cuadrado… Es más interesante ver los comentarios: http://cafematematico.com/2013/02/04/los-papeles-de-barcenas/
Quizás podeis usar y colaborar en el excel compartido que está pasando los datos del caso bárcenas a formatos computerizables. http://j.mp/Tu30Ua
Como han indicado, la ley de Benfor no es aplicable a datos con poca «horquilla» posibles.
Por ejemplo, los datos de altura de adultos en España empiezan casi todos por 1, y solo algunos por 2, pero ninguno por 3 (ni 4 ni 5 ni 6 ni 7 ni 8 ni 9) porque nadie mide ni 30 cm. ni 3 m., así que aquí no se espera que cumplan la ley.
En el caso de pagos en B, nadie espera ni que siga la ley de Benford ni la ley española, ninguna de las dos.
Se me ocurre una razón (igual equivocada) por la que prevalece el 2: el límite de dinero que puedes meter en una cuenta sin que Hacienda meta las narices.
Sergio,
Las series cuyos primeros dígitos siguen una distribución de Benford son aquellas en las que subyace un proceso de crecimiento.
Concretamente, TODAS las series monetarias cumplen la Ley de Benford por el fenómeno de la inflación (crecimiento de la base monetaria), que deprecia la unidad de cuenta cada año inexorablemente. Todo precio tiende a crecer en el tiempo conforme crece la cantidad de dinero en circulación.
Por el contrario, como bien indicaba un lector, la altura de las personas, el porcentaje de población ocupada o la hora a la que me levanto por la mañana no siguen una distribución de Benford porque no están sometidas a un proceso de crecimiento constante.
Abel,
Gracias por la actualización.
Saludos,
Miguel
Hola Abel, estás equivocado en que las únicas series que siguen la ley Benford son las que tienen crecimiento exponencial. Se observa en muchos otros ámbitos, por ejemplo en constantes fisicas, leyes de potencias, suma de distribuciones de probabilidad aleatorias… No es para nada una consecuencia únicamente del crecimiento exponencial sino de los sistemas de numeración posicionales en general.
En segundo lugar, explicar la abundancia de seises diciendo que los unos se transforman en seises es falso. 1000000 se transforman en 6000, pero 1164702 se transforma en 7000, y asi pasamos por 8000, 9000, 10000, 11000 y 12000 hasta llegar a los dos millones de pesetas. Como puedes observar, de nuevo abundancia de unos en el primer digito. La invariancia de escala es una bella propiedad de la ley de Benford.
Me parece muy bien que intentes educar a la gente en estos temas pero está claro que no es tu especialidad.
PD: envio el comentario por segunda vez porque creo que ha habido un problema la primera vez
Jaime,
He puesto énfasis en el caso de las series con distribución logarítmica (concretamente, log10, en la que el 1 es siempre el cambio de orden de magnitud) porque es el ejemplo más fácil de comprender y comprobar con una sencilla hoja de excel, como en el ejemplo que ponía en el artículo (bueno, y también para argumentar que los pagos en negro a lo largo del tiempo sí es razonable que sigan dicha distribución).
Respecto a las muchas otras regularidades empíricas y distribuciones (más bien suma de distribuciones) que parecen también ajustarse a dicha distribución, se salen del tema que estamos aquí tratando. He encontrado una presentación bastante completa y recomendable que trata todos estos temas:
http://www.lynceangroup.net/BenfordLynceanPresentation.pdf
“Benford is the distribution of all distributions”.
Respecto a la abundancia de “seises”, era un “artefacto” (me encanta este “false friend”) del cambio de escala en mitad de la serie; la invarianza respecto a la escala no implica necesariamente que la suma dos particiones de una serie en escalas distintas sigan la distribución.
Por último, respecto a su comentario “Me parece muy bien que intentes educar a la gente en estos temas pero está claro que no es tu especialidad”, por un lado decirle que dudo mucho que conozca mis habilidades y conocimientos: Sintetia nació como un divertimento para divulgar y sigue siéndolo, pero nuestras ocupaciones son otras; así que en segundo lugar me veo obligado a recordarle otra regularidad empírica bien conocida: “A nadie le caen bien los listillos”.
Yo no sé si no se está intentando matar moscas a cañonazos, con tanto análisis estadístico y test de chi-cuadrado… ¿Seguro que unos pagos más o menos fijos a un número limitado de personas deben seguir la ley de Benford? Supongamos que Bárcenas hubiera decidido la política del «café para todos», o sea, que todos los sobres contuvieran siempre 5.000 euros. Entonces seguro que se inclumplían al menos dos leyes: la de Benford y la Tributaria. ¿Qué demostraría entonces el sesudo análisis matemático? Me temo que lo mismo que el publicado en ABC: nada de nada…
Para Abel,
cito textualmente:
«Las series cuyos primeros dígitos siguen una distribución de Benford son aquellas en las que subyace un proceso de crecimiento.» FALSO, son aquellas y muchas mas, ver mi anterior comentario.
«muchas de las cantidades antes cercanas al millón de pesetas pasaron a expresarse en euros a partir de 2002, lo cual supuso convertir “unos” (por 1.000.000 pesetas) en “seises” (por 6.000 euros).» FALSO, por lo explicado en mi anterior comentario.
Y si me vas a decir que hay muchos seises porque habia muchos millones de pesetas redondos, entonces obviamente no hay ni proceso de crecimiento ni nada, son cifras elegidas a dedo y es estupido hacer tests estadisticos sobre la ley de Benford.
Aqui nadie pretende ser un listillo, simplemente a algunos nos gusta el rigor.
Jaime,
«[…]son cifras elegidas a dedo y es estupido hacer tests estadisticos sobre la ley de Benford.[…]»
Son cifras tan elegidas a dedo como el precio de, por ejemplo, un disco. Todo precio está determinado por muchos factores subyacentes, y los supuestos pagos en negro también. Casi todo precio parte de una referencia inicial, que puede remontarse 10 ó 10.000 años, y a partir de dicha referencia se ajusta en función de la inflación, costes, tecnología, etc.
En este caso se trata de pagos en negro por una actividad política. Trabajar en política tiene un coste alto. Para empezar, tienes que guardar tu honestidad en un cajón para el resto de tu vida. A mí, particularmente, eso me parece un coste excesivo. Como los salarios están regulados en proporción al resto de escalas salariales, muchos no aceptan trabajar en política si no reciben sobresueldos de distinta índole (unos legalmente y otros legalmente).
La cuantía de estos pagos, por lo tanto, aunque hayan sido elegidos aparentemente a dedo, no es arbitraria. De ser ciertos, vienen de siglos y siglos de corrupción de funcionarios públicos, los cuales solo eligen corromperse si la cuantía recibida supera un umbral respecto a la renta media.
No hay diferencia esencial ninguna respecto al balance de una empresa, que sí se analiza con Benford en busca de indicios.
Por último, si no quieres volver a parecer un listillo, argumenta con tranquilidad sobre el tema concreto y deja las alusiones personales para foros más apropiados.