La derrota del Real Madrid nos ha privado de presenciar uno de los más kafkianos finales concebibles, desde la teoría de juegos, para una liga de fútbol. De haber vencido, la clasificación en estos momentos habría sido: Atlético de Madrid 89, Real Madrid 87 y F.C. Barcelona 86 puntos. Y, aunque en el fútbol es tremendamente raro que se den situaciones en las que la estrategia óptima no sea jugar a ganar –salvo algunos empates que benefician a ambos equipos, que suelen darse por la lucha por evitar el descenso o en las primeras fases del Mundial o la Eurocopa-, la situación de la última jornada habría sido un divertido caso para la aplicación de la teoría de juegos.
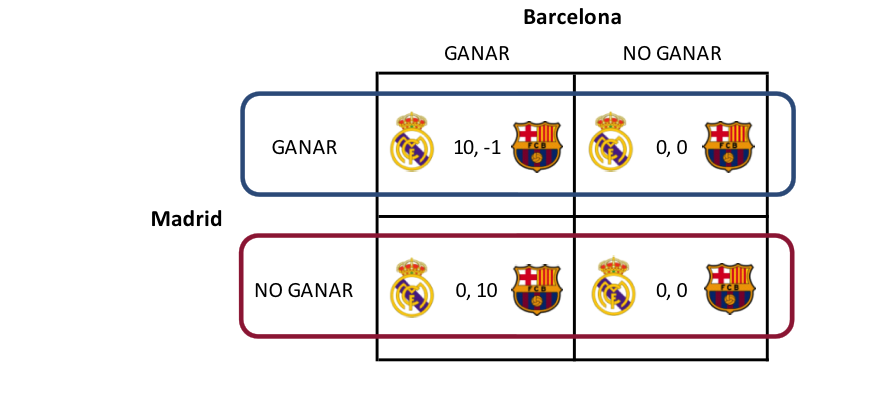
El siguiente diagrama resume los pagos finales –es decir, la utilidad recibida por cada equipo acabados ambos partidos- de todas las posibilidades de resultados (para hacernos la vida más fácil, el destino habría hecho que los empates fuesen idénticos a la derrota). Los supuestos de partida son que (1) ambos quieren ganar la liga, (2) que el Barcelona, de no ganar la liga, prefiere levemente que la gane el Atlético (dada su rivalidad extrema con el Real Madrid) y (3) que al Madrid le es indiferente que gane la Liga el Barcelona o el Atlético (la verdad es que, aunque el tercer supuesto pueda no ser real, en realidad no afecta a las estrategias del juego).
El diagrama expresa que:
– El Madrid recibe una utilidad 10 si ganan Madrid y Barcelona y 0 en cualquier otro caso.
– El Barcelona recibe una utilidad de 0 si pierde o empata, una utilidad de 10 si gana y el Madrid no gana… y una utilidad de -1 si gana pero el Madrid también, al contribuir a la victoria madridista en la Liga.
Una solución para la versión de juego simultáneo
Pues bien, incluso si se hubiese tratado de un juego simultáneo en el que ambos equipos pudiesen elegir el resultado con certeza, las estrategias resultantes no habrían estado nada claras. El Madrid habría tenido algo aparentemente parecido a una estrategia dominante, que sería GANAR, ya que 10 >= 0 y 0 >=0 –no estrictamente dominante, por la igualdad del 0=0-. Pero la clave está en que el Barcelona también sabe que dicha estrategia parece dominante para el Madrid: la decisión para el Barcelona se habría reducido al rectángulo azul, en el cual la estrategia dominante para el Barcelona, dada la del Madrid (GANAR), sería la de NO GANAR, ya que 0 > -1.
A su vez, el Madrid habría sido consciente de esta situación, por lo cual no podría jugar GANAR con un 100% de probabilidad, ya que perdería la Liga. Es decir, en el juego no existe un equilibrio de Nash, ya que no existe una estrategia en la que ambos equipos estén mejor independientemente de lo que haga el contrario. El Barcelona habría de creer que tiene alguna posibilidad de ganar la Liga para esforzarse. Y, de la misma forma, el Madrid ha de dar a entender al Barcelona que tiene alguna oportunidad. Curiosamente, existe un tipo de comportamiento, denominado estrategia mixta, la cual es una estrategia probabilística, en la que un equipo elige aleatoriamente una estrategia con un % de probabilidad y la otra con su probabilidad complementaria. Es decir, el Madrid habría de dar a entender que solo va a jugar al 80% ó 90% de sus posibilidades, lo cual da al Barcelona una oportunidad de ganar y un incentivo para jugar a ganar.
¿Cuál sería el resultado para un juego no simultáneo sino secuencial?
La representación más fiel del juego descrito no es, obviamente, simultánea –aunque podría haber algo de ello, anunciando alineaciones sub-óptimas-. Un juego secuencial representaría mejor la situación. El juego podría dividirse por ejemplo en dos partes, una hasta un cierto minuto de juego (el 70, por ejemplo) y otra hasta el final (suponiendo que se trata de un margen a partir del cual no se pueden adaptar ya estrategias).
En este caso, el Madrid, siguiendo el mismo razonamiento anterior, tendría muy poco incentivo para esforzarse en la primera parte del encuentro, o al menos a no obtener más de un gol de diferencia, ya que, de marcar dos goles rápidos, las posibilidades del Barcelona prácticamente se desvanecerían. Curiosamente, el Barcelona tampoco tendría un incentivo fuerte a esforzarse al 100% en esta primera parte, ya que un gol madrugador daría alas a los jugadores del Real Madrid, que verían el título más cerca –una cosa es que el Barcelona pueda no esforzarse lo suficiente atacando, pero otra distinta sería que se dejaran meter goles para que remontara el Atlético-. Quizás una ventaja mínima podría haber sido deseable para ambos equipos, pero lo lógico sería que se reservaran para los últimos 20 ó 30 minutos. Y esta opción, curiosamente, ¡es la que mejor representa, a pesar de tratar ahora el escenario secuencial, el equilibrio en “estrategias mixtas” descrito antes para el juego simultáneo! Ambos equipos prefieren ganar… pero no con una certidumbre absoluta.
No obstante, no teman. El Real Madrid ha conseguido, tras obtener 2 puntos de los 9 posibles en las tres últimas jornadas, privarnos de tan maquiavélico final de Liga. Y en el Barcelona – Atlético del próximo sábado sí que habrá un equilibrio de Nash: GANAR – GANAR.